Propiedades de las matrices simétricas. Sea A una matriz cuadrada de orden n y además simétrica, se cumple que: La matriz adjunta de A también es simétrica. Si A y B son dos matrices cuadradas de orden n y además simétricas, su suma también es simétrica, es decir, A=A t y B=B t entonces A+B= A t + B t = (A+B) t , lo mismo ocurre con la.. En matemáticas, particularmente en teoría de matrices, una matriz de banda o matriz con bandas es una matriz dispersa cuyas entradas distintas de cero están confinadas a una banda diagonal , que comprende la diagonal principal y cero o más diagonales a cada lado.. Formalmente, considere una matriz n × n A =( a i,j). Si todos los elementos de la matriz son cero fuera de una banda bordeada.

Almacenamiento Solar180

Dispositivos de almacenamiento

Gigabyte. Capacidad de almacenamiento en disco duro Euronics

Servicios de almacenamiento en la nube. Mind Map

LOGÍSTICA COMERCIAL PROPUESTA DE ALMACENAMIENTO
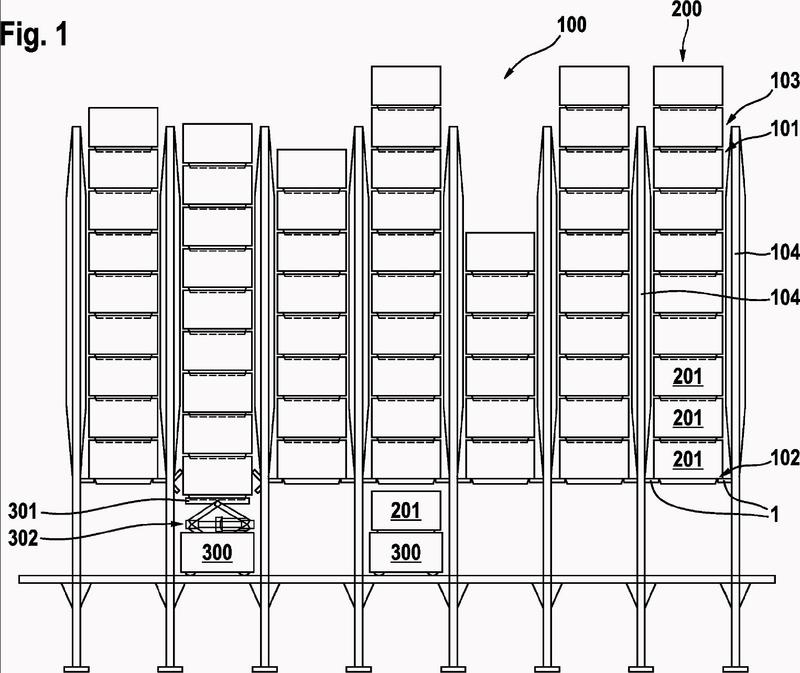
Dispositivo de sujeción y sistema de almacenamiento para…

cintas magnéticas Cinta magnética, Almacenamiento de datos, Modulos

Almacenamiento Online Al Lado Consultores
Redes Privadas Virtuales Almacenamiento compartido en red GFS2

Almacén con bpa y Asesoramiento Farmaceútico Almacenamiento BPA según

Cinta transportadora Banda Alimentaria calidad FDA

Miralrio

Smart Energy Consulting El almacenamiento de energía ligado a la red

CONJUNTOS Mind Map

Flowpack BFI 200
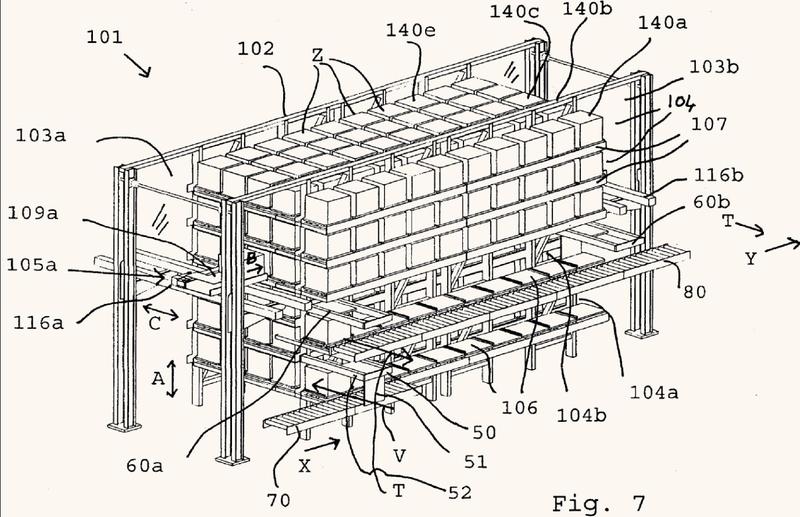
Sistema de almacenamiento y/o recogida de pedidos.

Almacenamiento eFuncionario

Almacenamiento en la nube Infográfia

Fuente dual simetrica YouTube

Medios de Almacenamiento Medios de Almacenamiento
Clasificación de las matrices según su forma en identidad, diagonal, bidiagonal, tridiagonal, triangular, traspuesta, adjunta, simétrica, antisimétrica, definida.. Resumimos las propiedades de la transposición de matrices A ↦ t A y cómo se relaciona con operaciones anteriores en el siguiente resultado. Proposición. La operación de transponer satisface: t ( t A) = A para toda A ∈ M m, n ( F). t ( A + B) = t A + t B para todas A, B ∈ M m, n ( F). t ( c A) = c t A si c ∈ F es un escalar y A ∈ M.