これまでとは違う考え方・手法を身に付けて,3点を通る2次関数を簡単に求める方法を身に付けましょう。具体的に次の問題を用いて説明していきます。. 高校数学Ⅰで学習する2次関数の単元から「平行移動して原点を通る」についてイチから解説しています。 ★講義資料はこちらから★>https://bit.ly/3M8U3gh 数スタのサイトはこちら>https://study-line.com/
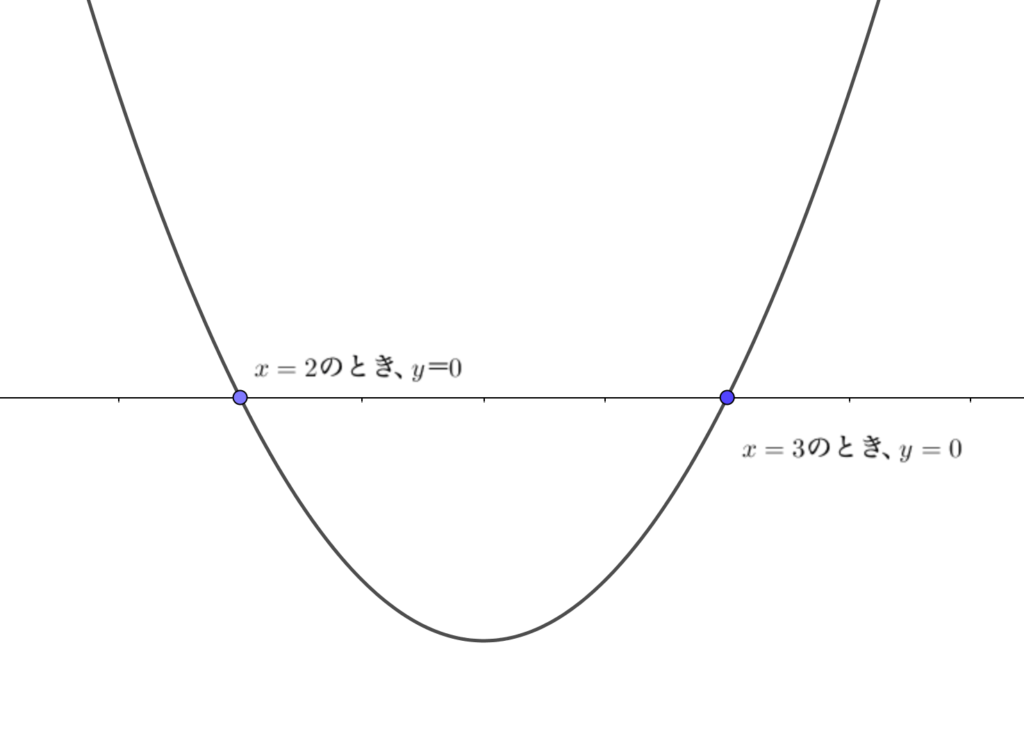
秒速理解!二次関数でよく使う変形と、使う意味や場面をまとめました! 青春マスマティック
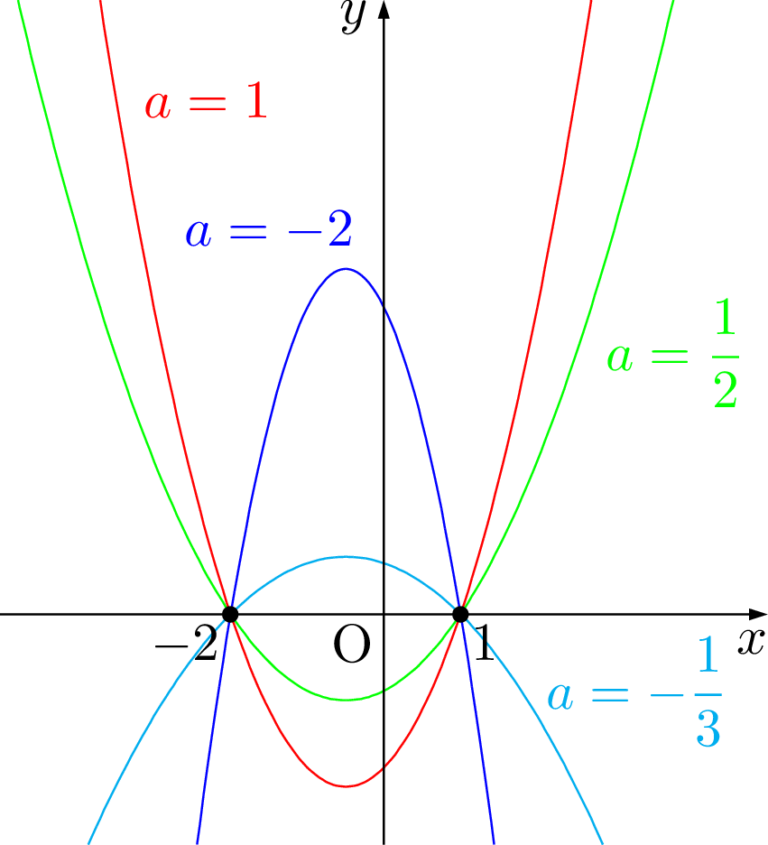
3点を通る2次関数(放物線)の方程式を簡単に求める方法とは? ページ 2 大学入試数学の考え方と解法

二次関数のグラフの平行移動
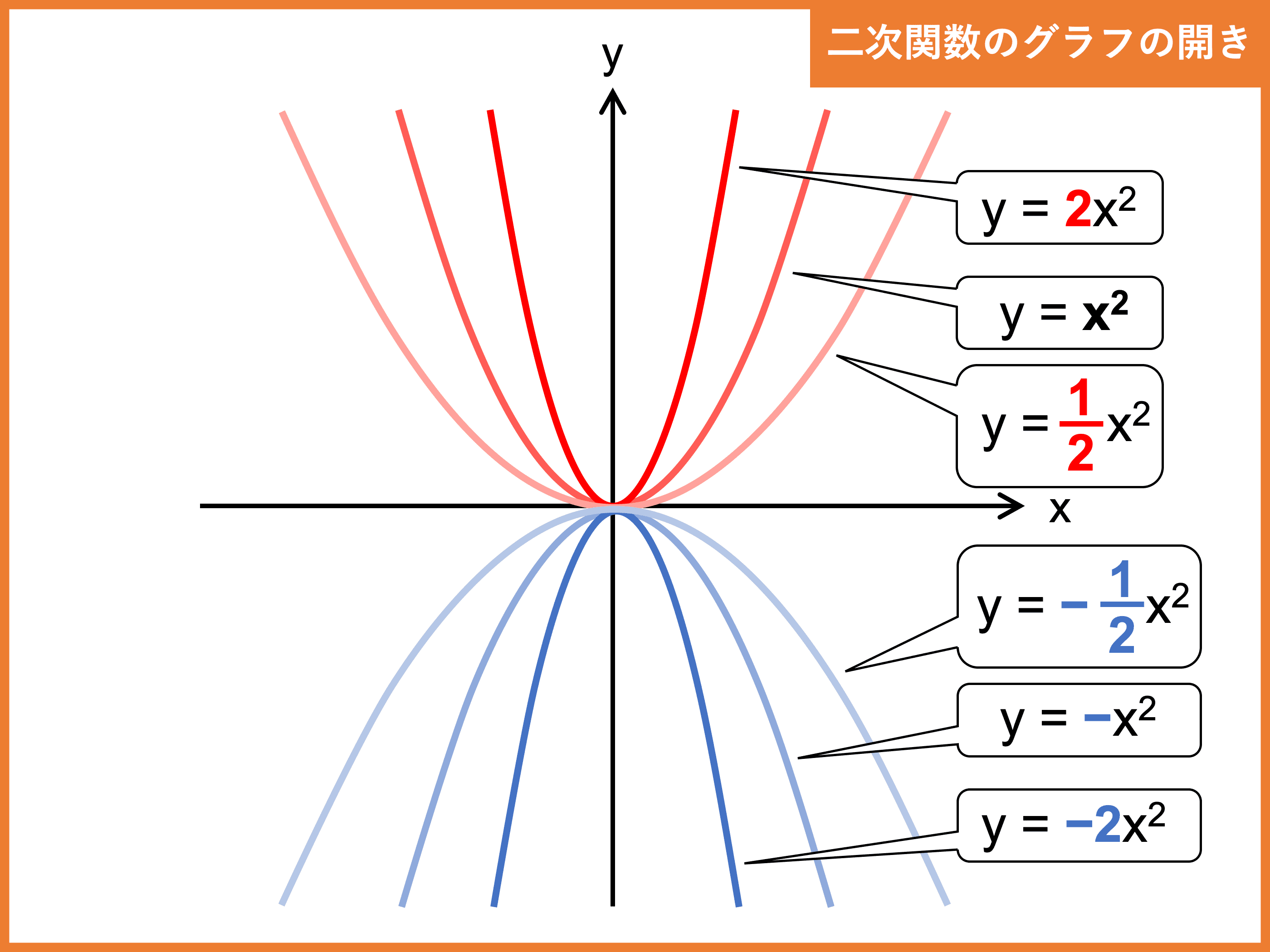
二次関数とは?公式や、最大値・最小値、決定の問題の解き方 受験辞典
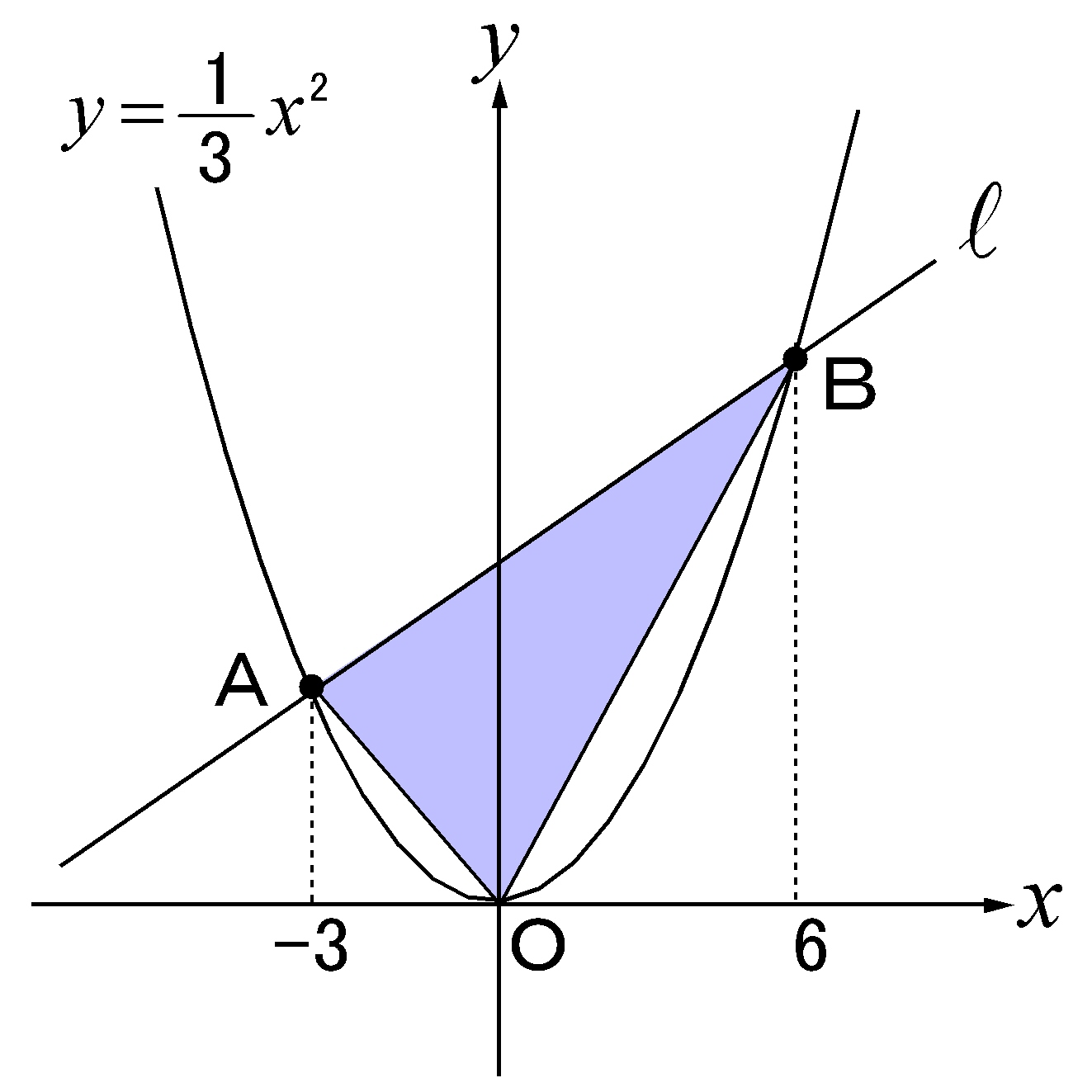
二次関数 グラフ 問題 中学 シモネタ

高校受験数学|解説動画|二次関数|点が放物線を動く時の軌跡|Quadratic function Trajectory when a point moves on a parabola
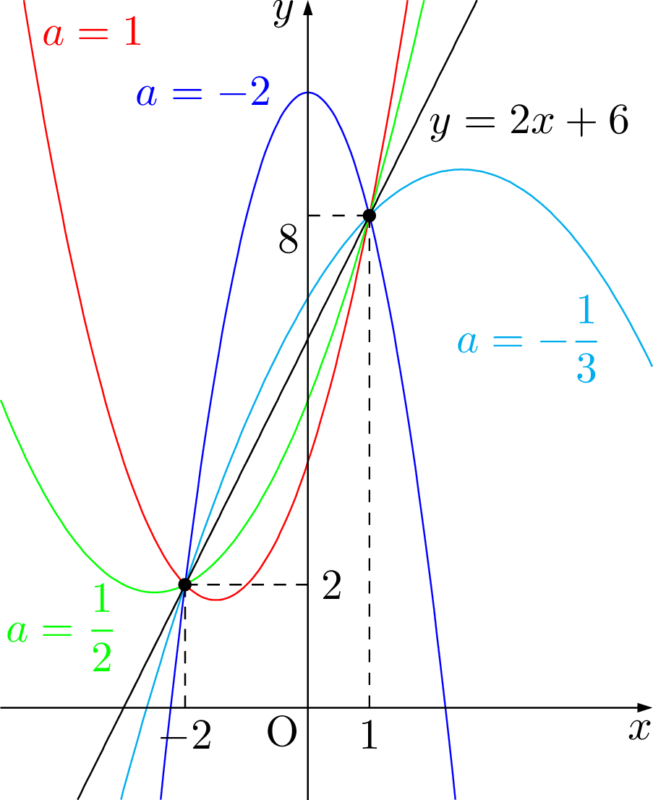
3点を通る2次関数(放物線)の方程式を簡単に求める方法とは? ページ 3 大学入試数学の考え方と解法
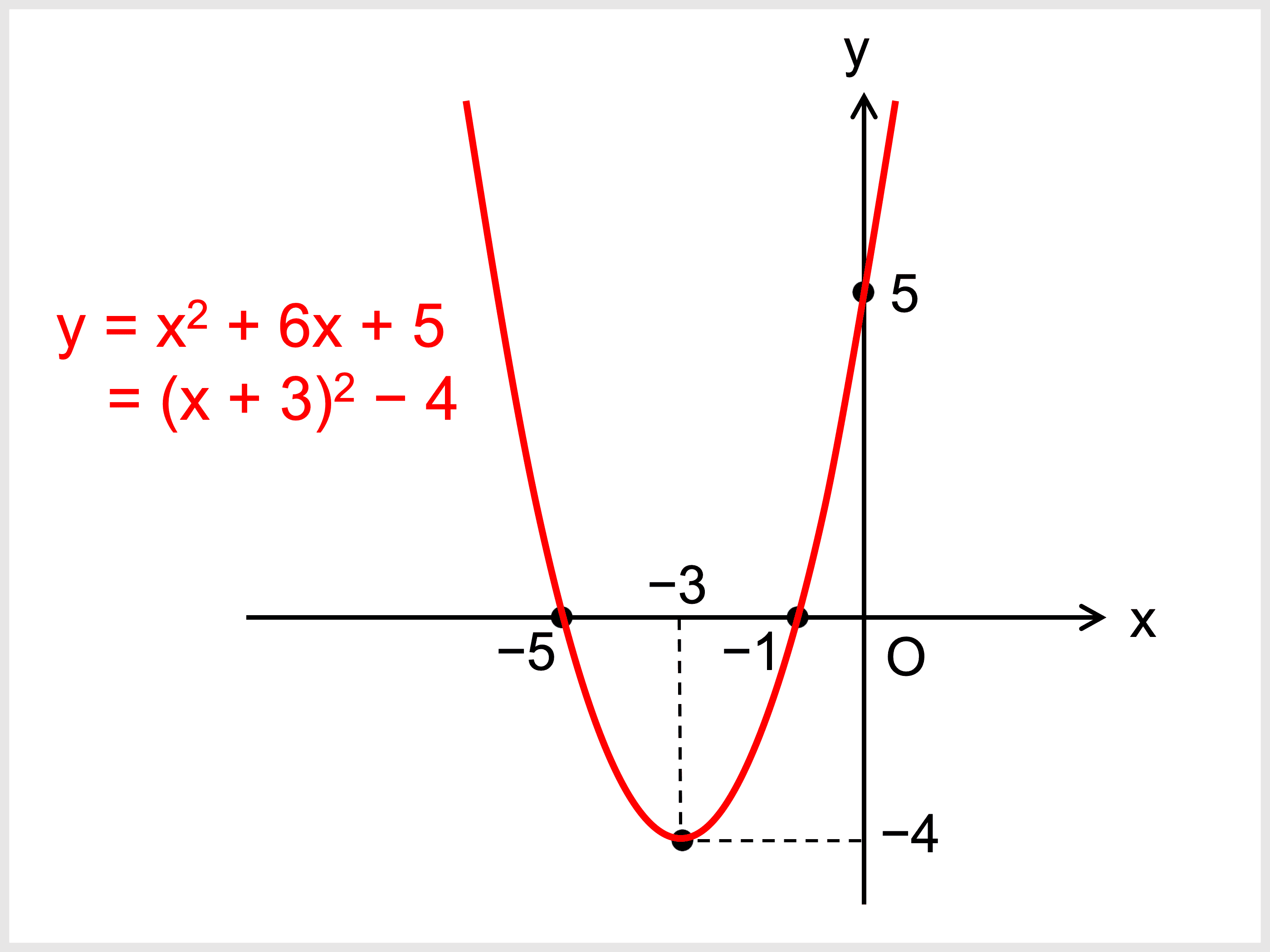
二次関数のグラフの書き方と、頂点・軸・切片の求め方 受験辞典

二次関数のグラフの書き方とグラフの問題を一気に紹介!|スタディクラブ情報局

2つの放物線の共有点を通る直線の式を10秒で出す YouTube
二次関数y=ax2の放物線にみられる5つの特徴 Qikeru:学びを楽しくわかりやすく
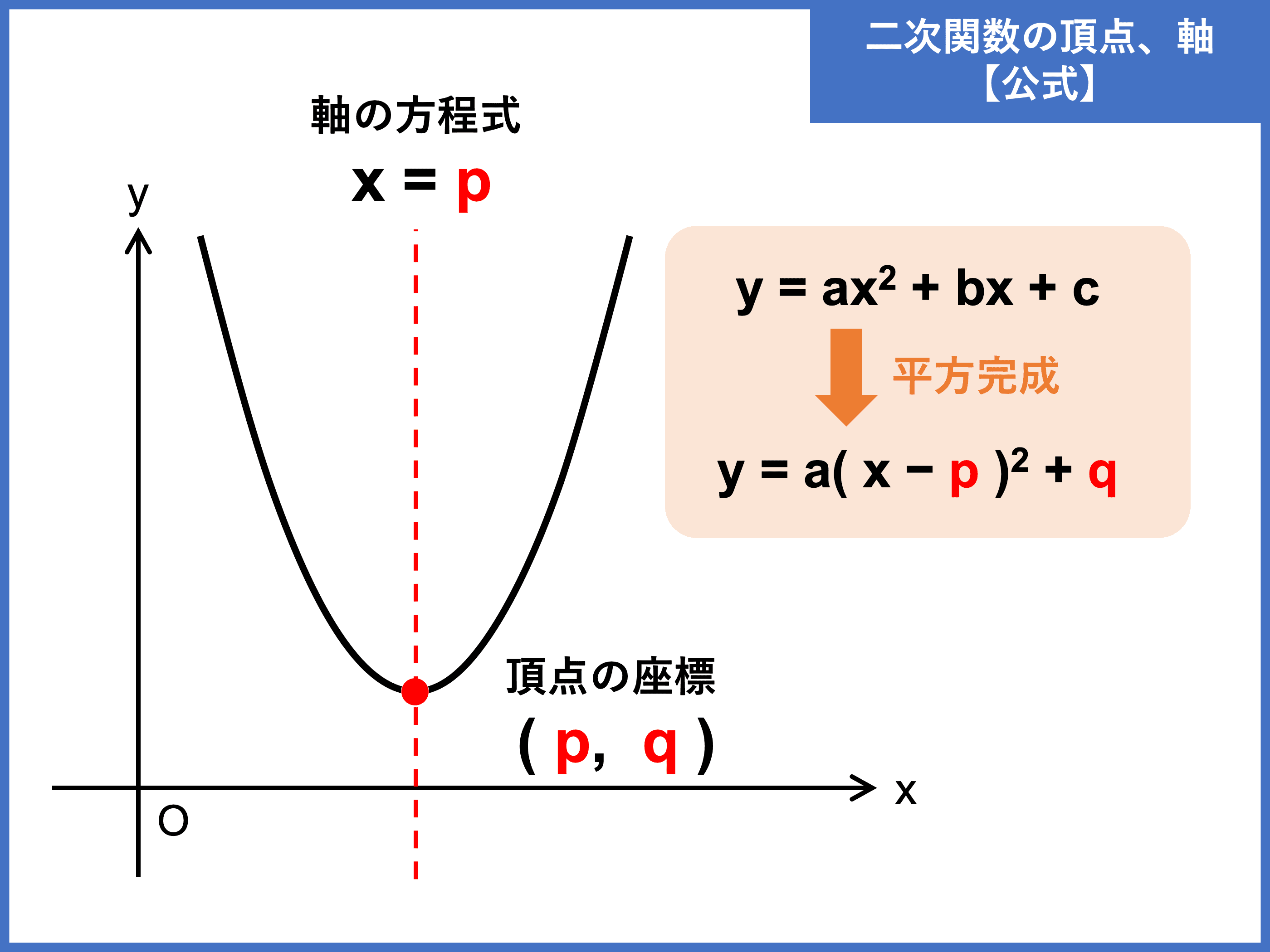
二次関数とは?公式や、最大値・最小値、決定の問題の解き方 受験辞典

二次関数の決定 大学受験の王道
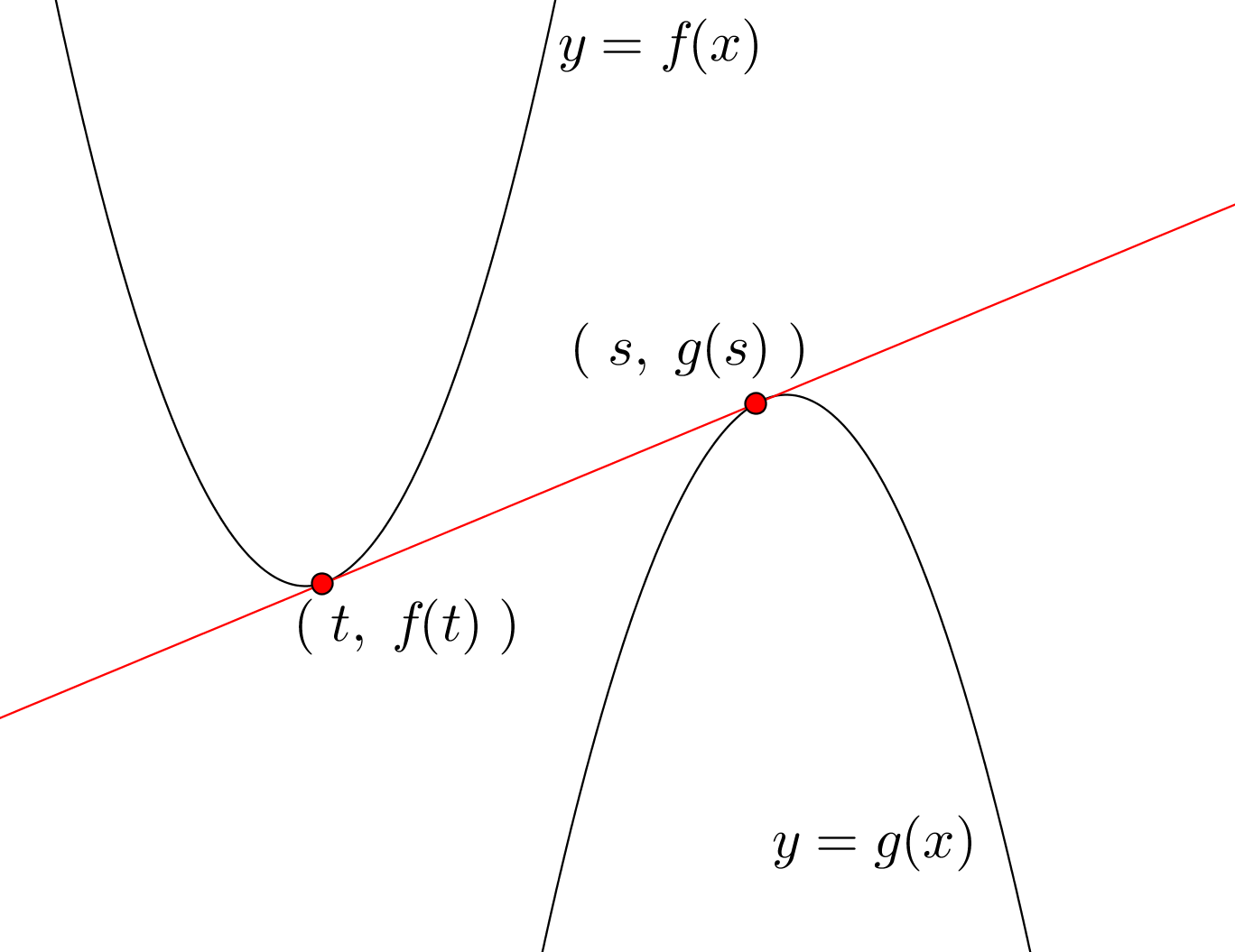
2つの曲線に共通な接線の方程式
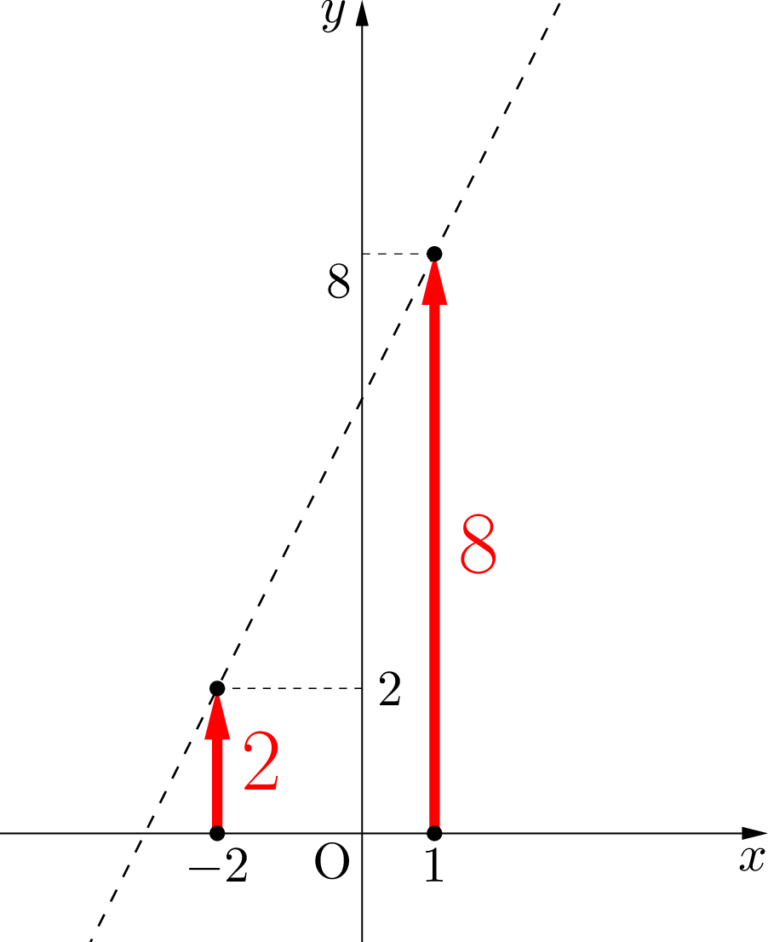
3点を通る2次関数(放物線)の方程式を簡単に求める方法とは? ページ 3 大学入試数学の考え方と解法
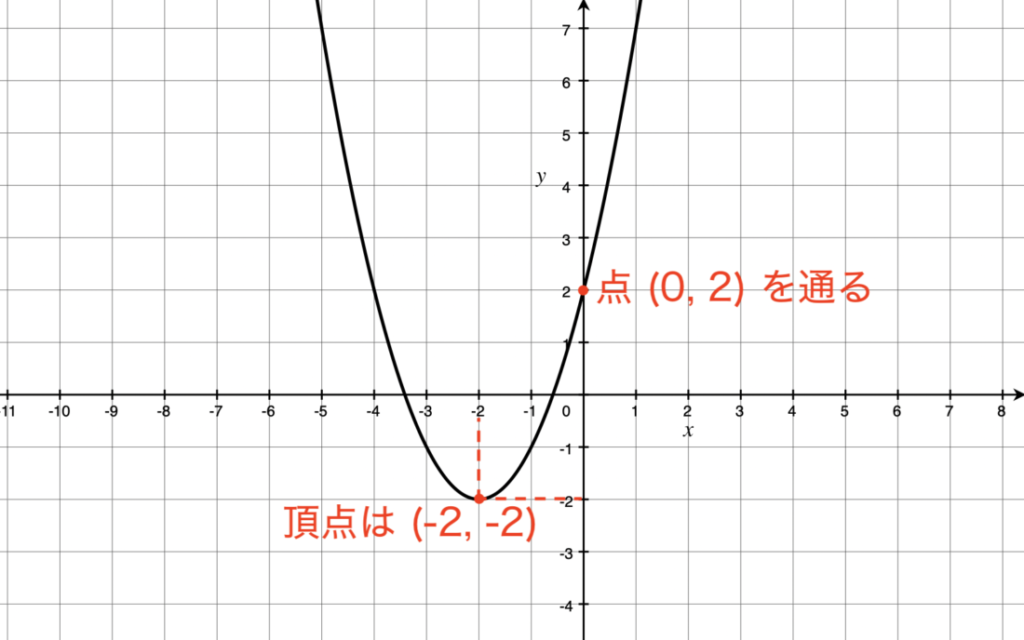
二次関数のグラフの書き方とグラフの問題を一気に紹介!|スタディクラブ情報局
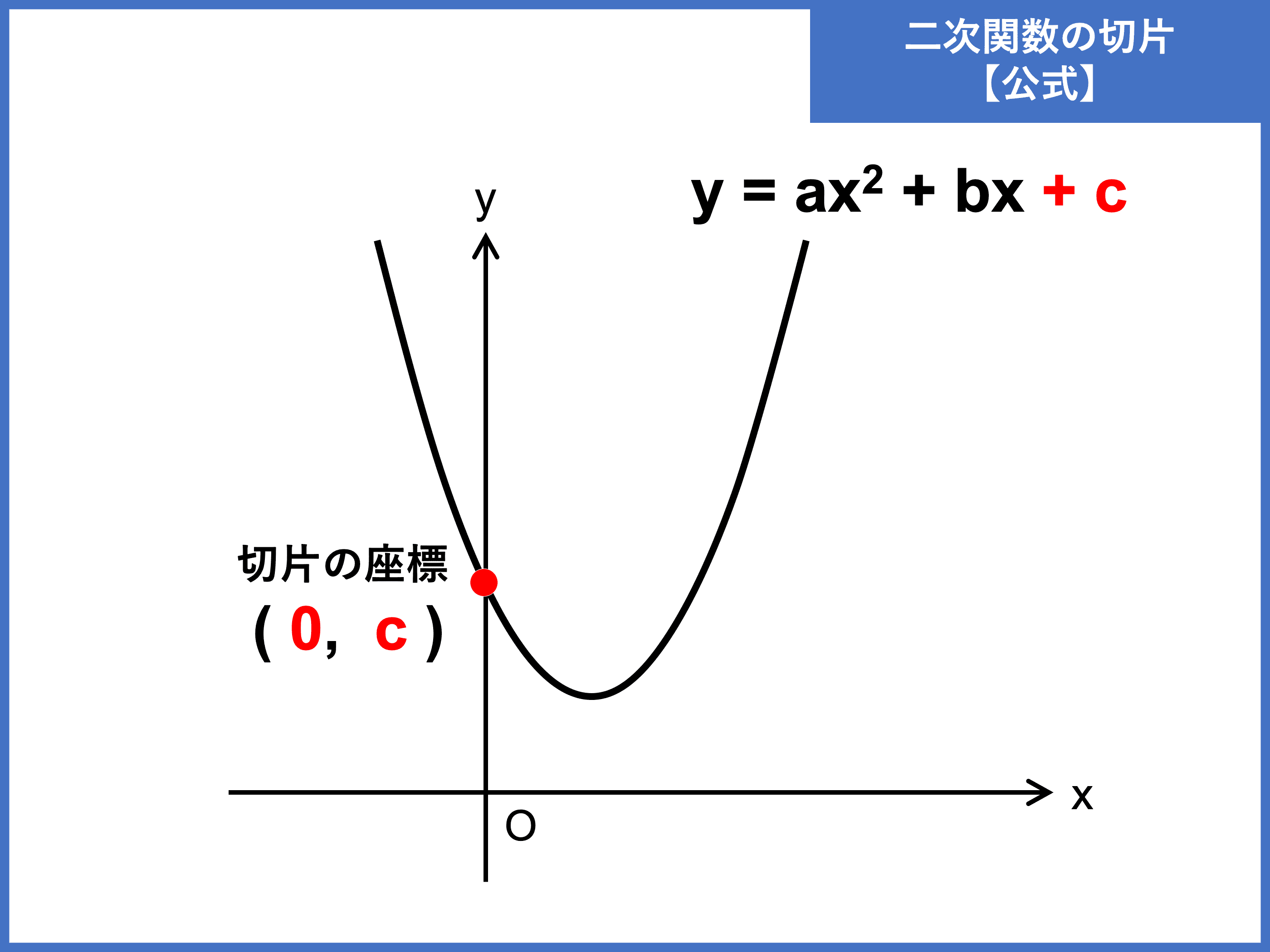
二次関数とは?公式や、最大値・最小値、決定の問題の解き方 受験辞典
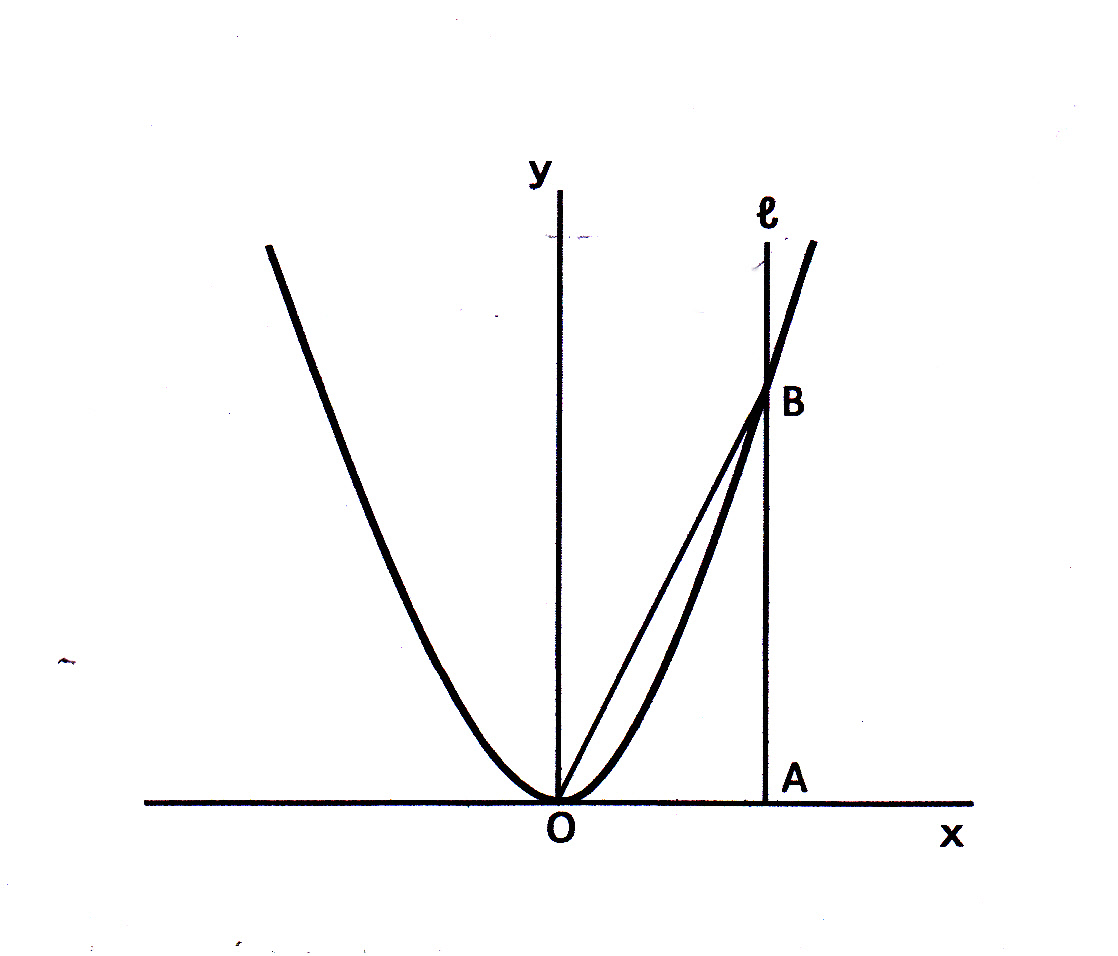
二次関数の利用の問題の解き方 グラフの問題(1) 現役塾講師のわかりやすい中学数学の解き方

二次関数のグラフの書き方とは?【頂点・軸・共有点の求め方】 遊ぶ数学

二次曲線とは 放物線の考え方と書き方 高校数学の知識庫
放物線上の2点を通る直線の式を簡単に求める方法を説明します。 この方法を知ることで,どんな放物線でも,その放物線上の2点を通る直線の式を簡単に求めることができるようになります。 知識を手に入れて計算を楽にしましょう。. まず、 (1, 0) ( 1, 0) を通るので、 x = 1 x = 1 、 y = 0 y = 0 を代入すると、. 0 = a + b + c 0 = a + b + c ・・・(1). 同様に、 (−3, 0) ( − 3, 0) を通るので、. 0 = 9a − 3b + c 0 = 9 a − 3 b + c ・・・(2). 同様に、 (2, −10) ( 2, − 10) を通るので、. −10 = 4a + 2b + c − 10.